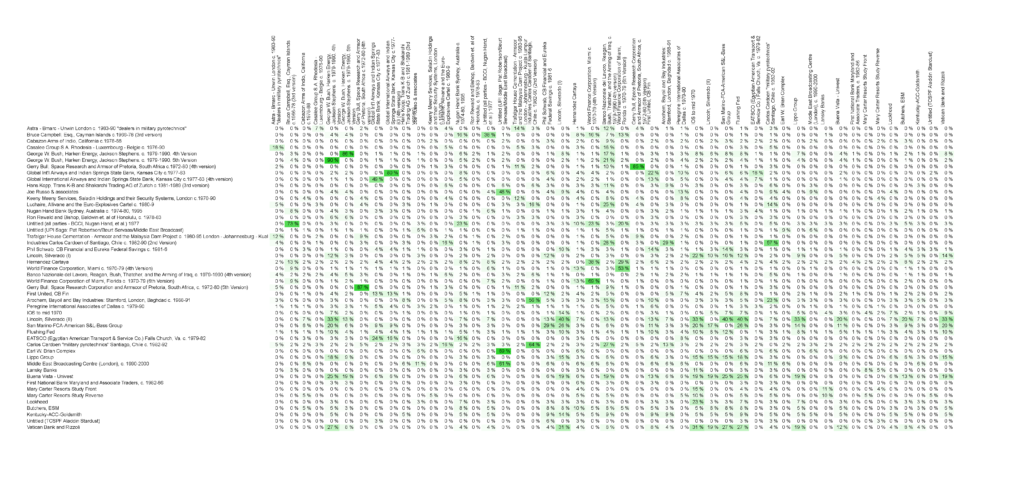
Calculating the relatedness of Lombardi drawings
We calculated a relatedness of the 48 networks that we have digitized. With this first experiment we are interested to look at how “similar” the drawings are. There are many measures on how graphs can be compared. We chose to look at the actors in the drawings first, not including their relations. So for our purposes it suffices that many actors simply appear in two drawing that we compare. We do not look at their structural similarity which would have to account for how the actors are connected by relations.
We know, that Lombardi started with small drawings that looked at various scandalous structures from different perspectives. Over time, the content of several such drawings was combined into larger ones, finally leading to the monumental drawings such as the huge one on BCCI.
The relatedness is rather given by some part-of relation than a traditional graph similarity. We hope to learn more about which works are related and perhaps predecessors of larger and later drawings.
With this intention compared all 48 networks pairwise. We calculated how many nodes appear in both of the respective two drawings. We could speak of an “overlap” in the actors of the two networks. We used our list of “aliases” of the same actors which raised the number of overlaps from 900+ to around 1600. We did not consider blank nodes and years. We weighted the number of nodes appearing in both networks considered with the respective total number of nodes in the drawing. We use that as a percentage. We do not compare networks with themselves, so no value is generated. Perhaps the table should show 100% in this case, rather than 0%. But this is a first experiment not more…
Technically, we wrote a script to generate a .csv file with a matrix of the percentages and then used Libre Office to visualize that matrix:
This is also downloadable as PDF. The raw data will be made available later on.
With this first experiment, one gets an impression of how this might lead to a genesis of drawings grouped by such a relatedness. There are many more options for calculations that we will explore.
As a side-note: The blank nodes might become interesting later. If we can identify later versions of a drawing with a blank node, then it might be that this node has been “uncovered” by Lombardi and named. For that we would have to look at the neighborhood of the blank nodes and find such a similar structure in a later version. This seems to be easily computable.